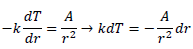Esercizio di trasporto/trasferimento di calore (heat transport/transfer exercise)

Anche io, come voi, mi sarei chiesto perché il titolo sia “Ingegneria Chimica in progress”; in effetti fino ad ora non ci azzecca niente, ma con il proseguire dei post si capirà.

Il primo post inerente al titolo è lo svolgimento di un semplicissimo esercizio di trasporto di calore. Sono umano e posso compiere errori, in tal caso scrivetelo nei commenti; i dati sono presi dal celeberrimo “PERRY’S CHEMICAL ENGINEERS’ HANDBOOK 8TH EDITION”.

La traccia dell’esercizio, di cui non posseggo alcun diritto è:

“All’interno di un elemento di combustibile nucleare di forma sferica (raggio R=15cm) viene generato del calore secondo la seguente funzione della coordinata radiale r:

La sfera è rivestita da uno strato di isolante di spessore δ=5cm ed è investita da aria alla temperatura di 10°C ed alla velocità di 5m/s.

Determinare la potenza termica che la sfera cede all’ambiente in condizioni stazionarie, il valore di temperatura sulla superficie dell’isolante, il valore del flusso termico per r=18cm. Indicare, inoltre, come si può pervenire alla stima del valore di temperatura in r=R. Commentare i risultati ottenuti.”.

SVOLGIMENTO

• ·         Alcune ipotesi: stato stazionario, linearità della conducibilità termica dell’isolante con la temperatura, trascurabilità di superfici solide a contatto con la sfera, uniformità delle proprietà di trasporto nel materiale, trasporto di calore radiale.

• ·         Rappresentazione grafica:

Determinare la potenza termica…

Per l’ipotesi di stato stazionario le derivate rispetto al tempo sono nulle e quindi non vi è accumulo; ciò ci porta a dire che tutto il calore generato deve essere smaltito verso l’esterno. Si noti che la generazione di calore varia solo lungo la coordinata r e risulta quindi identica per uguali distanze r; la funzione di generazione è espressa, come è possibile notare dalle unità di misura, per unità di volume.

Considerando un volume dV differenziale solo lungo la direzione r, in cui varia G(r):

La generazione, GEN, in tale volume sarà:

Si passa allora a fare l’integrale lungo tutto il volume della sfera di combustibile nucleare:

Sfruttando le proprietà degli integrali:

Scrivendo quanto detto in equazione di bilancio macroscopica:

-OUT+GEN=ACCUMULO, ACCUMULO=0→ OUT=GEN (eq.1)

Quindi la potenza termica che la sfera cede all’ambiente in condizioni stazionarie (OUT) è 144.9 W.

…il valore di temperatura sulla superficie dell’isolante…

Le condizioni stazionarie vengono raggiunte quando OUT=GEN, cioè quando sulla superficie esterna dell’isolante si raggiunge una temperatura tale da permettere di smaltire tutto il calore generato verso l’ambiente esterno alla sfera.

La legge del raffreddamento di Newton ci permette, a livello macroscopico, di tener conto di tutti i meccanismi di trasporto di calore che permettono il raffreddamento dell’oggetto per merito del fluido in movimento (convezione) che è a contatto con la superficie esterna; corrisponde a descrivere il flusso termico su una superficie lambita da un fluido mediante un coefficiente h che moltiplica una forza spingente, che nel nostro caso è la differenza tra la temperatura di parete e quella nel bulk della fase fluida(T_R+δ-T_∞).

L’eq. 1 può essere quindi riscritta:

Ovviamente la superficie interessata dallo scambio diretto di calore con il fluido è quella esterna all’isolante; l’eq. 2 diventa:

h è anche funzione di proprietà del fluido che a loro volta sono funzioni della temperatura T_R+δ, quindi h è funzione di T_R+δ; questa funzionalità, essendo complessa, ci porterà ad una risoluzione ricorsiva del problema.

h è espresso convenzionalmente attraverso correlazioni semi-empiriche che legano questo coefficiente a gruppi adimensionali tipici che caratterizzano la fluidodinamica e determinate proprietà del fluido (es. N_Re e N_Pr).

Per moto di fluidi intorno a sfere la correlazione è:

Dove k è la conducibilità termica, D è il diametro della sfera sommersa, v_∞ è la velocità del fluido non influenzata dalla presenza della sfera, µ è la viscosità, cp è il calore specifico a pressione costante su base massica; si noti che il pedice f indichi che le proprietà appartengono al fluido che investe la sfera e che queste vanno valutate in condizioni di film intermedio tra il bulk della fase fluida e lo strato di gas che ricopre l’isolante. Essendo la temperatura continua, la temperatura dello strato di fluido che riveste l’isolante e dell’isolante adiacente è la medesima:

Risulta quindi inutile far distinzione tra le due.

Essendo la temperatura variabile nella direzione radiale la condizione di film sarà:

Il nostro obiettivo è trovare  T_R+δ.

Di seguito verrà proposto il ciclo risolutivo.

Adesso si elencheranno formule e dati che ci permetteranno di ricavare alcune delle proprietà dell’aria a diverse temperature:

Primo ciclo:

La nuova T_f sarà molto prossima alla precedente, ci si aspetta che le proprietà varino così poco che la nuova T_R+δ sia, in pratica, 33°C; si prosegue comunque per completezza di calcolo.

Secondo ciclo:

La temperatura superficiale dell’isolante è  T_R+δ=32.9°C.

…il valore del flusso termico per r=18cm…

Il flusso per r=18cm può essere calcolato con un po’ di riflessione; essendo in stato stazionario ed in assenza di generazione (isolante), la portata termica in uscita è costante e sarà uguale per ogni superficie sferica di raggio r-esimo dell’isolante; ciò che cambia è il flusso in quanto risulta differente la superficie; quanto scritto può essere dimostrato attraverso un semplice bilancio termico su un  volume di isolante inizialmente piccolo e che portato al limite diventa differenziale lungo r (tale bilancio servirà per rispondere anche a successive richieste).

Rappresentazione grafica:

Bilancio:

IN-OUT=0

Dividendo per il volume di controllo 4πr²Δr e facendo il limite per Δr→0 si ottiene, per r≠0:

Quindi il prodotto q*r² risulta essere costante rispetto ad r (la costante è stata chiamata A); la portata termica è sostituendovi quanto ottenuto

Quindi il flusso termico per r=18cm è semplicemente portata fratto superficie:

…stima del valore di temperatura in r=R…

Per quanto è già stato detto T_R⁺= T_R^- e quindi basterà trovare la temperatura dell’isolante per r=R.

Per fare ciò ricaviamo il profilo di temperatura imponendo opportune condizioni al contorno; la costante A è deducibile da eq.6: 

Sostituendo la legge di Fourier in eq.5 si ottiene:

Sostituendo la funzione “k(T)=b*T+c”, poiché k è per ipotesi lineare, integrando tra i generici valori e la condizione al contorno trovata in precedenza (r=0.20m, T=32.9°C) si ottiene:

Si noti che, avendo imposto come condizione al contorno un flusso (o meglio una portata termica), questo può essere legato al gradiente di temperatura solo tramite la conducibilità che risulterà, necessariamente, un grado di libertà da saturare nel profilo di temperatura.

In parole povere, tutto il calore generato è dissipato per l’ipotesi di stazionarietà: qualsiasi materiale permette ciò, mantenendo all’interno una temperatura dipendente dalla sua conducibilità.

 si ottiene dunque:

Valutando il secondo membro in r=0.15m e risolvendo l’equazione di secondo grado, prendendo il risultato positivo:

N.B. Alcuni risultati potrebbero uscire diversi per motivi di approssimazione differente nei calcoli precedenti, le considerazioni (commenti) sono sparse per tutto il post, IF SOMEONE NEEDS THE TRANSLATION OF THE EXERCISE IN ENGLISH, TELL ME... I WILL DO IT.